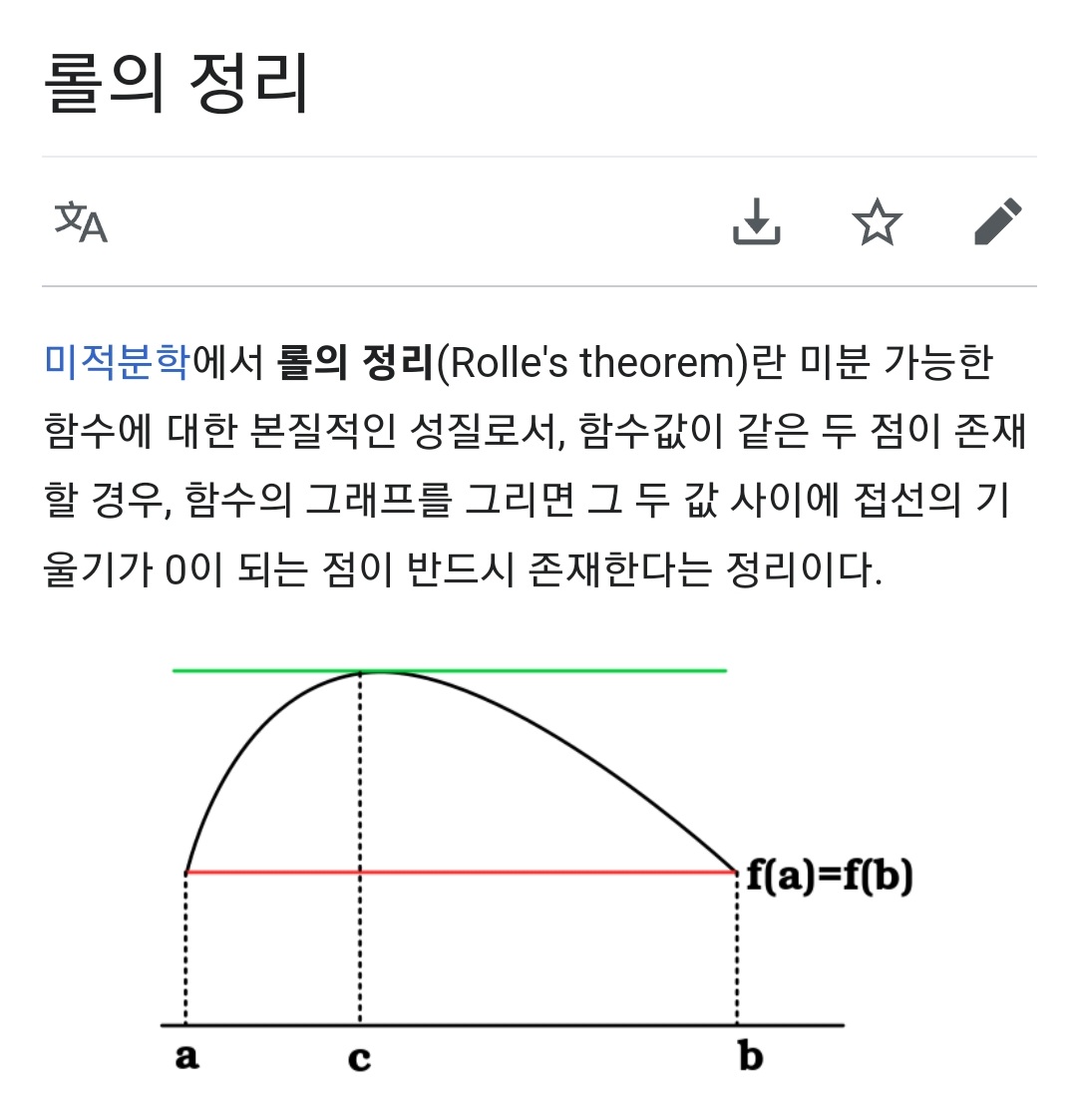
. 출처: Wikipedia 닫힌구간 [a,b]에서 정의된 연속함수 f가 (a,b)에서 미분가능하다. 만약에 f(a)=f(b)라는 조건이 있다면 항상 구간 [a,b]에서 함수의 최댓값 혹은 최솟값이 존재한다. 그 값에 대응되는 점 c가구간 (a,b) 안에 존재하며, 그 점에서 함수의 미분값은 0이다. 즉 f(a)=f(b) 이면 항상 미분값이 0이되는 점 c가 구간 (a,b)안에 존재한다. 내 증명의 전략은 이렇다. 1. [a,b] 는 compact set이면 f([a,b]) 도 compact set이다. 2. f([a,b])는 최댓값과 최솟값을 갖는다. 3. f(a)=f(b)라면, 반드시 그 구간안에 최댓값이나 최솟값중 하나가 되는 f(c)가 구간 (a,b) 안에 존재한다. 4. darboux의 정리에 ..