.
출처: Wikipedia
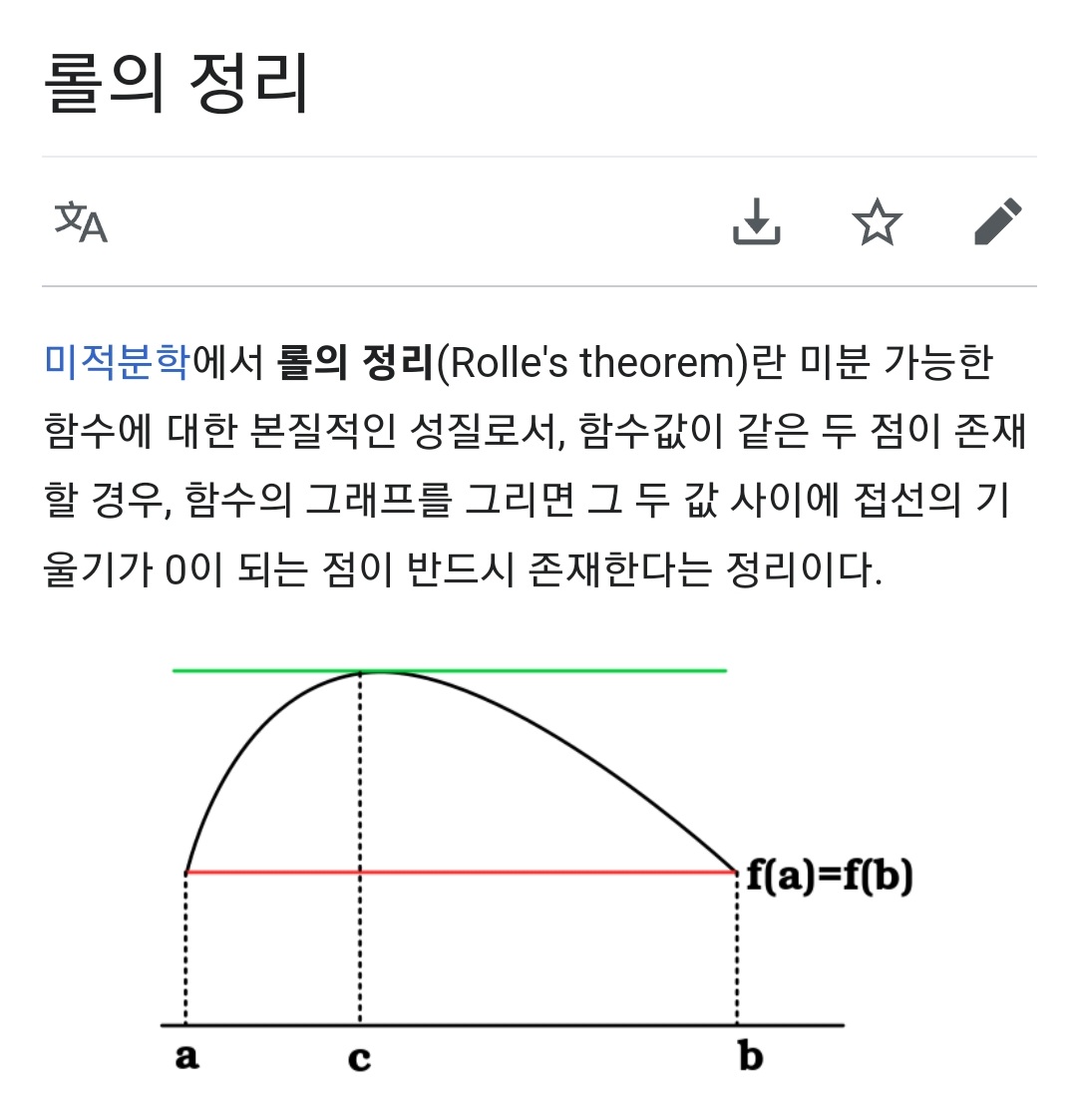
닫힌구간 [a,b]에서 정의된
연속함수 f가 (a,b)에서 미분가능하다.
만약에 f(a)=f(b)라는 조건이 있다면
항상 구간 [a,b]에서 함수의 최댓값 혹은 최솟값이 존재한다.
그 값에 대응되는 점 c가구간 (a,b) 안에 존재하며, 그 점에서 함수의 미분값은 0이다.
즉 f(a)=f(b) 이면
항상 미분값이 0이되는 점 c가 구간 (a,b)안에 존재한다.
내 증명의 전략은 이렇다.
1. [a,b] 는 compact set이면 f([a,b]) 도 compact set이다.
2. f([a,b])는 최댓값과 최솟값을 갖는다.
3. f(a)=f(b)라면, 반드시 그 구간안에 최댓값이나 최솟값중 하나가 되는 f(c)가 구간 (a,b) 안에 존재한다.
4. darboux의 정리에 의해 c에서 f의 미분값은 0이다.


가정: 만약에 Rf가 bounded set이 아니라면, 증가 하면서 최댓값이 없는 수열 (Xn)이 Rf에 포함되어있을것이다.
그렇다면 Xn 을 함수값으로 같는 수열 Yn 이 구간 [a,b] 에 포함될테고,
Bolzano–Weierstrass 정리에 따르면
Yn은 수렴하는 부분수열 Ynk를 갖는다.
그 극한값을 Y라 하자
f는 연속함수이므로 f(Ynk)의 극한값은 f(Y) 와 같다.
Xnk는 수렴하는 수열이 된다.
그렇다면 처음 상정한 증가하면서 최댓값이 없는 수열 Xn은 존재하지 않는다. 그러므로 Rf는 bounded set이다.

Rf가 closed라는 말은
Rf에 포함된 수렴하는 수열의극한값 또한 Rf에 포함됨을 뜻한다.
원소가 전부 Rf에 포함되나, 극한값X는 Rf에 포함되지않는 수렴하는 수열(Xn)이 존재한다고 해보자.
bounded를 보일때와 마찬가지로 f(Yn)=Xn인 수열( Yn)이 [a,b]에 포함되고
Yn의 수렴하는 부분수열 (Ynk) 가 극한값Y를 갖는다고 하면, 수렴하는 수열의 부분수열은 원래 수열과 같은 극한값을 갖는다. 고로 Xnk는 극값 X를 갖는다.
f(Y)=X이므로
결국 X는 Rf에 포함이된다.
그러므로 원소가 Rf에 포함되는 수렴하는 수열은, 극값도 Rf에 포함이된다.
즉 Rf는 closed 이다.

Rf는 closed set이므로
자신의 sup을 포함한다.
이 sup을 k 라고 하자
f(c)=k 인 c가 구간 [a,b] 안에존재 하므로
함수 f는 구간 [a,b] 안에서 최댓값 maximum value를 갖는다.
마찬가지로 Rf는 inf도 포함하고 함수 f는 구간 [a,b]안에서 최솟값 minimum value를 갖는다.
그래서 함수의 치역 f([a,b])는 항상 최댓값과 최솟값을 둘다 갖는다.
f(a)=f(b)가 최댓값이자 최솟값이면
함수 f는 구간에서 상수함수이므로
구간 (a,b) 내 임의의 점에서 미분값이 0이다
f가 구간에서 상수함수가 아닌경우
f(a)=f(b)가 최솟값인 경우에는 최댓값에 대응되는 c가 구간 (a,b) 안에 들어있다.
마찬가지로 f(a)=f(b)가 최댓값인경우에는 최솟값에 대응되는 c가 구간 (a,b) 안에 들어있다.
f(c)가 최댓값인경우
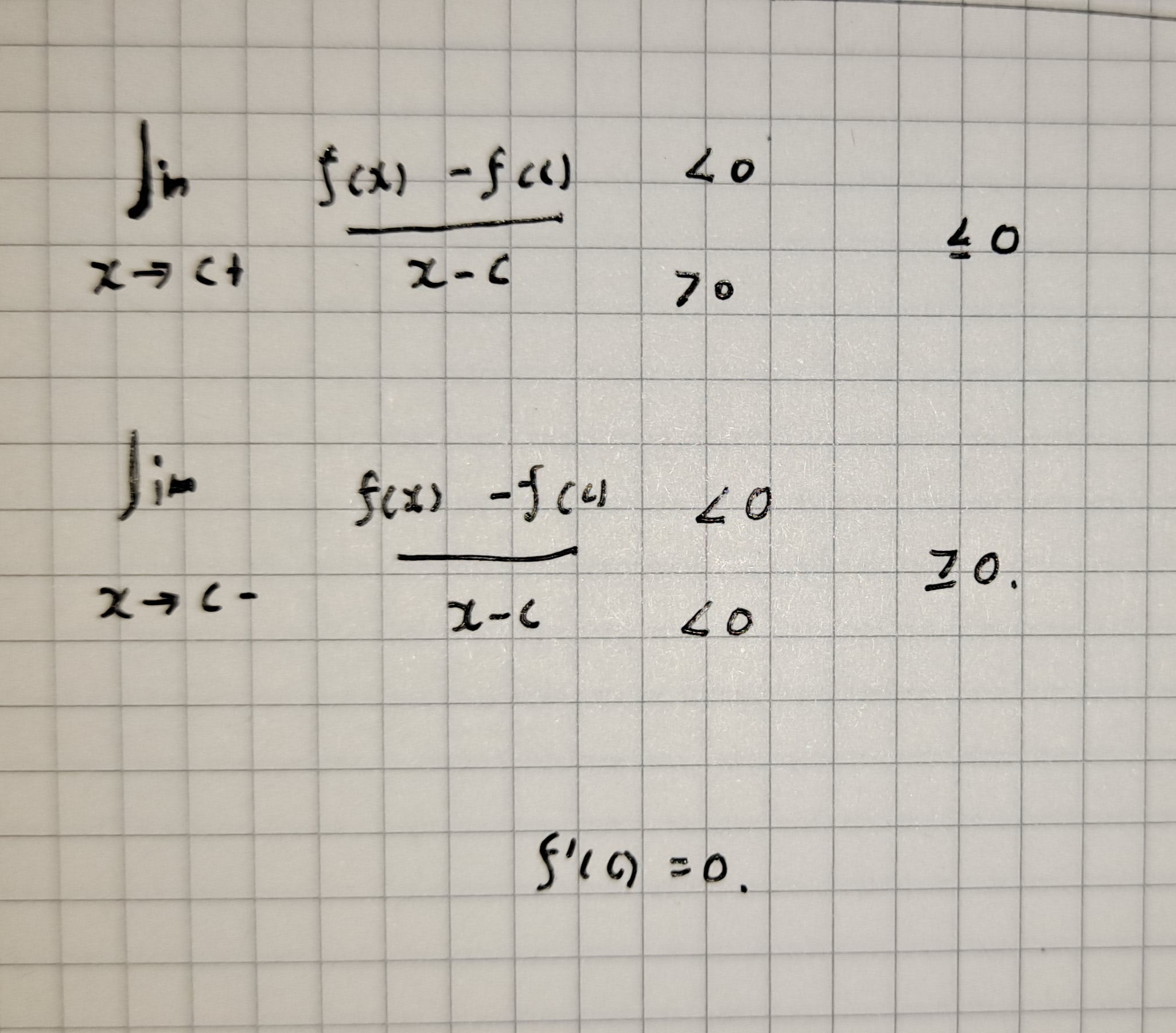
c에서의 미분값은 0임을 알 수있다.
최솟값인 경우에도 분자의 부호만 바꾸어 똑같이 보일수있다.
g(x)= f(x) + [f(b)-f(a)]/(b-a)x
라 두면 g는 연속, 미분가능하며 g(b)-g(a)=0 이므로
미분값이 0인 c가 있음을 알수있다.
고로 평균값정리는 쉽게보여진다.
폰으로 끄적이니까 한시간이 넘게걸렸다....
빠르게 작업하는 방법을 알아봐야겠다.
수식은 나중에 아이패드를 사거나 레이텍을 연습하게되면
다시 올려야겠다
혹시 궁금한게있으시거나 오류를 발견하시면 댓글로 알려주세요